
- SAP Community
- Products and Technology
- Technology
- Technology Blogs by Members
- Vector Search in pure ABAP (any DB)
Technology Blogs by Members
Explore a vibrant mix of technical expertise, industry insights, and tech buzz in member blogs covering SAP products, technology, and events. Get in the mix!
Turn on suggestions
Auto-suggest helps you quickly narrow down your search results by suggesting possible matches as you type.
Showing results for
Alice_V
Participant
Options
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
11-27-2023
1:26 PM
Hello, my name is Alice, and I have about two decades of experience in ABAP/SAP and a lifelong passion for programming.
I wanted to share my recent PoC project/library with you.
It's a simple yet fast Vector DB implemented entirely in ABAP (and one table, any DB).
It turned out that a) it is possible and b) it is "good enough" to replace external solutions in specific scenarios.
Let me show you 😃
GitHub:oisee/zvdb: ABAP Vector Search Library (github.com)
So, what problem are we trying to solve?
The library serves as a straightforward, in-house alternative to third-party vector databases. This is particularly useful if you require semantic search capabilities directly on the ABAP application server.
This tool can enhance your RAG (Retrieval Augmented Generation) applications, along with other heuristics.
(Disclaimer: This project was completed before the recent OpenAI developer conference, meaning it predates their introduction of "Assistant API" and "GPTs." While the latest OpenAI API now supports knowledge-based RAG without external VDBs, this solution may still be relevant, especially for RAG implementations using the Azure OpenAI API).
(More info on RAG: text video)
RAG is the technique that is powering the “chat with your documents” scenario:
The practicality of the ABAP Vector Search Library will be validated based on the following criteria:
Local Query Time: The time required to perform a local query using the library should be significantly less than when it calls an external third-party Vector Database, typically hosted on platforms like Azure. This ensures that the library offers a practical alternative to using external services.
But the slowest part of RAG - is the response of the LLM itself, so if Query will take ~10% of the LLM response time, it is still OK.
Volume-Based Criteria: The library should be able to handle a substantial volume of vectors in the database. As a reference point, a minimal threshold for practicality could be the ability to efficiently query a dataset equivalent to several books, with the average book size being approximately 300 pages. If the library can efficiently query more than this volume (e.g., 3000 vectors or more), it can be deemed "good enough" for practical usage.
These criteria ensure that the library is efficient in terms of query time and can handle reasonably large datasets, making it a valuable tool for various applications.
Let's start with data:
Our embedding vectors are 1536-dimensional, ranging from -1 to 1. Keep in mind that these vectors may not always be unit vectors.
1536-dimensional embedding by the model ada-002:
The measure of similarity between two vectors - Cosine similarity
And it can be calculated as dot product (or scalar product):
[a1,a2,a3,a4] • [b1,b2,b3,b4] = a1*b1 + a2*b2 + a3*b3 + a4*b4
i.e. comparison of two 1536d vectors requires:
=> 3072 operations for one comparison.
Starting point: brute force search
The most straightforward way to find something is a brute force search: the query vector must be compared with all the vectors in DB. Result of the each comparison – the cosine similarity can be interpreted as “rank”. The result must be sorted, and then the top k-nearest neighbours will be the query's result.
Path A - Quantization:
1536-dimensional embedding by ada-002:
Quantized:
1b: sign is enough:
Path A - Bitwise Operations
Bitwise multiplication is XOR: With 0 and 1 as +1 and -1:
Summation is just a bit-counting operation (+1 if 0 and -1 if 1):
01010 xor 10101 = 11111, bit counting: -5
(max distance – vectors have nothing in common)
11100 xor 11100 = 00000, bit counting: +5
(min distance – vectors identical)
¡10111 xor 11111 = 01000, bit counting: +4 – 1 = 3
(some distance – almost identical – one bit of difference)
Let’s do the BF search:
Calculate DP for:
sort the resulting rank and compare the order of results.
The order for the rank 1536 (equal) to 512 (not yet perpendicular, but far enough to stop worrying) is stable.
What if we can mark similar vectors that are close? There is a function for that! 😃
Spatial HASH function: Similar vectors are likely to end up with the same or similar hash. (i.e. closer in lower-dimensional space)
1536d is exceptionally high:
If 64d (wheat and chessboard problem) is just 8x8 “image”.
Then1536d is a 48x32 “image”.
We can slice hyperspace into two parts with a random vector:
If it is “below” – 1 if it is “above” 0
As many vectors – as many digits in the hash.
8 vectors will give us 8-bit (1 byte) hash which we can use as an index, which will be "good enough" for about 256*256 = 65536 vectors in the DB.
To widen the selection, we can fetch not just exact match but neighbours of hamming distance 1 or 2.
Handling Non-Uniform Distribution
But what if our vectors are not uniformly distributed? Then, the random hyperplane method might be irrelevant - similar vectors might be clustered together.
In this case, we can use vectors from the dataset as hyperplanes:
Any other methods to speed up the search?
Fast ranking We can use Dot Products between HASHes of two vectors to make ranking faster “quick force” instead of “brute force”.
Some stats:
Optimization: initially, it was ~3000μs for one floating-point unquantized comparison; using 1b quantization and bitwise operation, it was optimized down to ~20μs, so we easily can perform the dot product (i.e., do brute force search) for ~50000 vectors per second.
For RAG with the context window of 32k, it is more than enough ^_^
GitHub:oisee/zvdb: ABAP Vector Search Library (github.com)
Alice Vinogradova is a seasoned ABAP/SAP professional with a rich background in programming, spanning from Z80 assembly to modern data processing techniques. Her passion lies in exploring and optimizing complex systems, bridging traditional computing with innovative technological advancements.
I wanted to share my recent PoC project/library with you.
It's a simple yet fast Vector DB implemented entirely in ABAP (and one table, any DB).
It turned out that a) it is possible and b) it is "good enough" to replace external solutions in specific scenarios.
Let me show you 😃
TL;DR:
GitHub:oisee/zvdb: ABAP Vector Search Library (github.com)
What problem are we trying to solve
So, what problem are we trying to solve?
The library serves as a straightforward, in-house alternative to third-party vector databases. This is particularly useful if you require semantic search capabilities directly on the ABAP application server.
This tool can enhance your RAG (Retrieval Augmented Generation) applications, along with other heuristics.
(Disclaimer: This project was completed before the recent OpenAI developer conference, meaning it predates their introduction of "Assistant API" and "GPTs." While the latest OpenAI API now supports knowledge-based RAG without external VDBs, this solution may still be relevant, especially for RAG implementations using the Azure OpenAI API).
(More info on RAG: text video)
RAG is the technique that is powering the “chat with your documents” scenario:
- Slice documents into chunks
- Generate vector embedding for these chunks
- When answer the question, search for semantically relevant chunks in DB,
- Inject semantically relevant chunks into the Prompt, something like:
Considering only the information below:
###
{chunk01}
{chunk02}
{chunk03}
###
please provide a response to the following request:
{query from user}
Validation: "GOOD ENOUGH"
The practicality of the ABAP Vector Search Library will be validated based on the following criteria:
- Local Query Time less Call to External VDB – excellent
- Local Query Time less ~10% of the LLM response time - OK
- Volume-Based Criteria: Should handle at least ~10 books
- => 10 * 300 pages = 3000 embeddings
Local Query Time: The time required to perform a local query using the library should be significantly less than when it calls an external third-party Vector Database, typically hosted on platforms like Azure. This ensures that the library offers a practical alternative to using external services.
But the slowest part of RAG - is the response of the LLM itself, so if Query will take ~10% of the LLM response time, it is still OK.
Volume-Based Criteria: The library should be able to handle a substantial volume of vectors in the database. As a reference point, a minimal threshold for practicality could be the ability to efficiently query a dataset equivalent to several books, with the average book size being approximately 300 pages. If the library can efficiently query more than this volume (e.g., 3000 vectors or more), it can be deemed "good enough" for practical usage.
These criteria ensure that the library is efficient in terms of query time and can handle reasonably large datasets, making it a valuable tool for various applications.
Understanding Data
Let's start with data:
Our embedding vectors are 1536-dimensional, ranging from -1 to 1. Keep in mind that these vectors may not always be unit vectors.
1536-dimensional embedding by the model ada-002:
- [-7.912499859230593e-05, -0.022456586360931396, 0.018665215000510216, -0.02411365509033203, 0.0009089018567465246, 0.031524062156677246, -0.027944795787334442, 0.008245570585131645, -0.006893403362482786, -0.018983371555805206, 0.009723675437271595, 0.01825426146388054 ... ]
The measure of similarity between two vectors - Cosine similarity
And it can be calculated as dot product (or scalar product):
[a1,a2,a3,a4] • [b1,b2,b3,b4] = a1*b1 + a2*b2 + a3*b3 + a4*b4
i.e. comparison of two 1536d vectors requires:
- 1536 multiplications
- 1536 additions
=> 3072 operations for one comparison.
Starting point: brute force search
The most straightforward way to find something is a brute force search: the query vector must be compared with all the vectors in DB. Result of the each comparison – the cosine similarity can be interpreted as “rank”. The result must be sorted, and then the top k-nearest neighbours will be the query's result.
Pathways to Optimization
- A - Faster calculations
- B - Fewer calculations
Path A - Quantization:
- Quantize -1…+1 into 8bit (fine)
- Quantize -1…+1 into 4bit (coarse)
- Quantize -1…+1 into 1bit (extreme)

quantization, fixed point arithmetic
1536-dimensional embedding by ada-002:
Quantized:
- 8b: [-1, -3, 4, -4, 2, 6, -4, 3, -1, -3, 3, 4, 2, 2, -3, 2, 4, 3, 2, 3, -1, 5, 4, 4, -2, 4, 3, …] -127…+127
- 3b: [-1, -1, 2, -1, 2, 2, -1, 2, -1, -1, 2, 2, 2, 2, -1, 2, 2, 2, 2, 2, -1, 2, 2, 2, -1, 2, 2, …] -3…-3
- 1b: [-1, -1, 1, -1, 1, 1, -1, 1, -1, -1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, -1, 1, 1, 1, -1, 1, 1, …] -1..+1
1b: sign is enough:
- 0 – is positive
- 1 – negative
Path A - Bitwise Operations
Bitwise multiplication is XOR: With 0 and 1 as +1 and -1:
- 0 xor 0 = 0 (+1 * +1 = +1 )
- 1 xor 1 = 0 (-1 * -1 = -1 )
- 0 xor 1 = 1 (1 * -1 = -1 )
- 1 xor 0 = 1 (-1 * 1 = -1 )
Summation is just a bit-counting operation (+1 if 0 and -1 if 1):
01010 xor 10101 = 11111, bit counting: -5
(max distance – vectors have nothing in common)
11100 xor 11100 = 00000, bit counting: +5
(min distance – vectors identical)
¡10111 xor 11111 = 01000, bit counting: +4 – 1 = 3
(some distance – almost identical – one bit of difference)
Validation: 1b vs 8b vs fp
Let’s do the BF search:
Calculate DP for:
- Q1b
- Q8b
- Floating Point
sort the resulting rank and compare the order of results.
The order for the rank 1536 (equal) to 512 (not yet perpendicular, but far enough to stop worrying) is stable.
Path B – NARROWING SELECTION
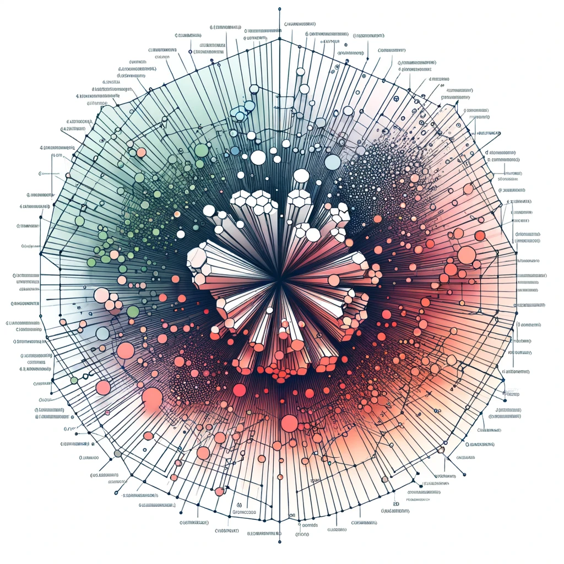
visualisation of vector clusters in 3d space
What if we can mark similar vectors that are close? There is a function for that! 😃
Spatial HASH function: Similar vectors are likely to end up with the same or similar hash. (i.e. closer in lower-dimensional space)
1536d is exceptionally high:
If 64d (wheat and chessboard problem) is just 8x8 “image”.
Then1536d is a 48x32 “image”.
Random hyperplanes method
We can slice hyperspace into two parts with a random vector:
If it is “below” – 1 if it is “above” 0
As many vectors – as many digits in the hash.
8 vectors will give us 8-bit (1 byte) hash which we can use as an index, which will be "good enough" for about 256*256 = 65536 vectors in the DB.
To widen the selection, we can fetch not just exact match but neighbours of hamming distance 1 or 2.
Handling Non-Uniform Distribution
But what if our vectors are not uniformly distributed? Then, the random hyperplane method might be irrelevant - similar vectors might be clustered together.
In this case, we can use vectors from the dataset as hyperplanes:
- Pickup random vector
- Find Nearest
- Furthest
- Mid-Point
- Mid-Point is a highly likely perpendicular vector – good enough to be the next axis of the index (hash function)
Any other methods to speed up the search?
Fast ranking We can use Dot Products between HASHes of two vectors to make ranking faster “quick force” instead of “brute force”.
Stats
Some stats:
Optimization: initially, it was ~3000μs for one floating-point unquantized comparison; using 1b quantization and bitwise operation, it was optimized down to ~20μs, so we easily can perform the dot product (i.e., do brute force search) for ~50000 vectors per second.
For RAG with the context window of 32k, it is more than enough ^_^
Source code: $ZVDB.
GitHub:oisee/zvdb: ABAP Vector Search Library (github.com)
About the Author:
Alice Vinogradova is a seasoned ABAP/SAP professional with a rich background in programming, spanning from Z80 assembly to modern data processing techniques. Her passion lies in exploring and optimizing complex systems, bridging traditional computing with innovative technological advancements.
- SAP Managed Tags:
- ABAP Development,
- SAP HANA
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
Labels in this area
-
"automatische backups"
1 -
"regelmäßige sicherung"
1 -
"TypeScript" "Development" "FeedBack"
1 -
505 Technology Updates 53
1 -
ABAP
18 -
ABAP API
1 -
ABAP CDS Views
4 -
ABAP CDS Views - BW Extraction
1 -
ABAP CDS Views - CDC (Change Data Capture)
1 -
ABAP class
2 -
ABAP Cloud
3 -
ABAP DDIC CDS view
1 -
ABAP Development
5 -
ABAP in Eclipse
3 -
ABAP Platform Trial
1 -
ABAP Programming
2 -
abap technical
1 -
abapGit
1 -
absl
2 -
access data from SAP Datasphere directly from Snowflake
1 -
Access data from SAP datasphere to Qliksense
1 -
Accrual
1 -
action
1 -
adapter modules
1 -
Addon
1 -
Adobe Document Services
1 -
ADS
1 -
ADS Config
1 -
ADS with ABAP
1 -
ADS with Java
1 -
ADT
2 -
Advance Shipping and Receiving
1 -
Advanced Event Mesh
3 -
Advanced formula
1 -
AEM
1 -
AI
8 -
AI Launchpad
1 -
AI Projects
1 -
AIML
10 -
Alert in Sap analytical cloud
1 -
Amazon S3
1 -
Analytic Models
1 -
Analytical Dataset
1 -
Analytical Model
1 -
Analytics
1 -
Analyze Workload Data
1 -
annotations
1 -
API
1 -
API and Integration
4 -
API Call
2 -
API security
1 -
Application Architecture
1 -
Application Development
5 -
Application Development for SAP HANA Cloud
3 -
Applications and Business Processes (AP)
1 -
Artificial Intelligence
1 -
Artificial Intelligence (AI)
5 -
Artificial Intelligence (AI) 1 Business Trends 363 Business Trends 8 Digital Transformation with Cloud ERP (DT) 1 Event Information 462 Event Information 15 Expert Insights 114 Expert Insights 76 Life at SAP 418 Life at SAP 1 Product Updates 4
1 -
Artificial Intelligence (AI) blockchain Data & Analytics
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise Oil Gas IoT Exploration Production
1 -
Artificial Intelligence (AI) blockchain Data & Analytics Intelligent Enterprise sustainability responsibility esg social compliance cybersecurity risk
1 -
AS Java
1 -
ASE
1 -
ASR
2 -
Asset Management
2 -
Associations in CDS Views
1 -
ASUG
1 -
Attachments
1 -
Authentication
1 -
Authorisations
1 -
Automating Processes
1 -
Automation
2 -
aws
2 -
Azure
2 -
Azure AI Studio
1 -
Azure API Center
1 -
Azure API Management
1 -
B2B Integration
1 -
Background job
1 -
Backorder Processing
1 -
Backpropagation
1 -
Backup
1 -
Backup and Recovery
1 -
Backup schedule
1 -
BADI_MATERIAL_CHECK error message
1 -
Bank
1 -
Bank Communication Management
1 -
BAS
1 -
basis
2 -
Basis Monitoring & Tcodes with Key notes
2 -
Batch Management
1 -
BDC
1 -
Best Practice
1 -
BI
1 -
bitcoin
1 -
Blockchain
3 -
bodl
1 -
BOP in aATP
1 -
BOP Segments
1 -
BOP Strategies
1 -
BOP Variant
1 -
BPC
1 -
BPC LIVE
1 -
BTP
15 -
BTP AI Launchpad
1 -
BTP Destination
2 -
Business AI
1 -
Business and IT Integration
1 -
Business application stu
1 -
Business Application Studio
1 -
Business Architecture
1 -
Business Communication Services
1 -
Business Continuity
2 -
Business Data Fabric
3 -
Business Fabric
1 -
Business Partner
13 -
Business Partner Master Data
11 -
Business Technology Platform
2 -
Business Trends
4 -
BW4HANA
1 -
CA
1 -
calculation view
1 -
CAP
4 -
Capgemini
1 -
CAPM
1 -
Catalyst for Efficiency: Revolutionizing SAP Integration Suite with Artificial Intelligence (AI) and
1 -
CCMS
2 -
CDQ
13 -
CDS
2 -
CDS Views
1 -
Cental Finance
1 -
Certificates
1 -
CFL
1 -
Change Management
1 -
chatbot
1 -
chatgpt
3 -
CICD
1 -
CL_SALV_TABLE
2 -
Class Runner
1 -
Classrunner
1 -
Cloud ALM Monitoring
1 -
Cloud ALM Operations
1 -
cloud connector
1 -
Cloud Extensibility
1 -
Cloud Foundry
4 -
Cloud Integration
6 -
Cloud Platform Integration
2 -
cloudalm
1 -
communication
1 -
Compensation Information Management
1 -
Compensation Management
1 -
Compliance
1 -
Compound Employee API
1 -
Configuration
1 -
Connectors
1 -
Consolidation
1 -
Consolidation Extension for SAP Analytics Cloud
3 -
Control Indicators.
1 -
Controller-Service-Repository pattern
1 -
Conversion
1 -
Corrective Maintenance
1 -
Cosine similarity
1 -
CPI
1 -
cryptocurrency
1 -
CSI
1 -
ctms
1 -
Custom chatbot
3 -
Custom Destination Service
1 -
custom fields
1 -
Custom Headers
1 -
Customer Experience
1 -
Customer Journey
1 -
Customizing
1 -
cyber security
5 -
cybersecurity
1 -
Data
1 -
Data & Analytics
1 -
Data Aging
1 -
Data Analytics
2 -
Data and Analytics (DA)
1 -
Data Archiving
1 -
Data Back-up
1 -
Data Flow
1 -
Data Governance
5 -
Data Integration
2 -
Data Quality
13 -
Data Quality Management
13 -
Data Synchronization
1 -
data transfer
1 -
Data Unleashed
1 -
Data Value
9 -
Database and Data Management
1 -
database tables
1 -
Databricks
1 -
Dataframe
1 -
Datasphere
3 -
Datasphere Delta
1 -
datenbanksicherung
1 -
dba cockpit
1 -
dbacockpit
1 -
Debugging
2 -
Defender
1 -
Delimiting Pay Components
1 -
Delta Integrations
1 -
Destination
3 -
Destination Service
1 -
Developer extensibility
1 -
Developing with SAP Integration Suite
1 -
Devops
1 -
digital transformation
1 -
Disaster Recovery
1 -
Documentation
1 -
Dot Product
1 -
DQM
1 -
dump database
1 -
dump transaction
1 -
e-Invoice
1 -
E4H Conversion
1 -
Eclipse ADT ABAP Development Tools
2 -
edoc
1 -
edocument
1 -
ELA
1 -
Embedded Consolidation
1 -
Embedding
1 -
Embeddings
1 -
Emergency Maintenance
1 -
Employee Central
1 -
Employee Central Payroll
1 -
Employee Central Time Off
1 -
Employee Information
1 -
Employee Rehires
1 -
Enable Now
1 -
Enable now manager
1 -
endpoint
1 -
Enhancement Request
1 -
Enterprise Architecture
1 -
Enterprise Asset Management
2 -
Entra
1 -
ESLint
1 -
ETL Business Analytics with SAP Signavio
1 -
Euclidean distance
1 -
Event Dates
1 -
Event Driven Architecture
1 -
Event Mesh
2 -
Event Reason
1 -
EventBasedIntegration
1 -
EWM
1 -
EWM Outbound configuration
1 -
EWM-TM-Integration
1 -
Existing Event Changes
1 -
Expand
1 -
Expert
2 -
Expert Insights
2 -
Exploits
1 -
Fiori
16 -
Fiori App Extension
2 -
Fiori Elements
2 -
Fiori Launchpad
2 -
Fiori SAPUI5
13 -
first-guidance
1 -
Flask
2 -
FTC
1 -
Full Stack
9 -
Funds Management
1 -
gCTS
1 -
GenAI hub
1 -
General
3 -
Generative AI
1 -
Getting Started
1 -
GitHub
11 -
Google cloud
1 -
Grants Management
1 -
groovy
2 -
GTP
1 -
HANA
6 -
HANA Cloud
2 -
Hana Cloud Database Integration
2 -
HANA DB
2 -
Hana Vector Engine
1 -
HANA XS Advanced
1 -
Historical Events
1 -
home labs
1 -
HowTo
1 -
HR Data Management
1 -
html5
9 -
HTML5 Application
1 -
Identity cards validation
1 -
idm
1 -
Implementation
1 -
Improvement Maintenance
1 -
Infuse AI
1 -
input parameter
1 -
instant payments
1 -
Integration
3 -
Integration Advisor
1 -
Integration Architecture
1 -
Integration Center
1 -
Integration Suite
1 -
intelligent enterprise
1 -
Internal Table
1 -
IoT
2 -
Java
1 -
JMS Receiver channel ping issue
1 -
job
1 -
Job Information Changes
1 -
Job-Related Events
1 -
Job_Event_Information
1 -
joule
4 -
Journal Entries
1 -
Just Ask
1 -
Kafka
1 -
Kerberos for ABAP
10 -
Kerberos for JAVA
9 -
KNN
1 -
Launch Wizard
1 -
Learning Content
3 -
Life at SAP
5 -
lightning
1 -
Linear Regression SAP HANA Cloud
1 -
Live Sessions
1 -
Loading Indicator
1 -
local tax regulations
1 -
LP
1 -
Machine Learning
4 -
Marketing
1 -
Master Data
3 -
Master Data Management
15 -
Maxdb
2 -
MDG
1 -
MDGM
1 -
MDM
1 -
Message box.
1 -
Messages on RF Device
1 -
Microservices Architecture
1 -
Microsoft
1 -
Microsoft Universal Print
1 -
Middleware Solutions
1 -
Migration
5 -
ML Model Development
1 -
MLFlow
1 -
Modeling in SAP HANA Cloud
9 -
Monitoring
3 -
MPL
1 -
MTA
1 -
Multi-factor-authentication
1 -
Multi-Record Scenarios
1 -
Multilayer Perceptron
1 -
Multiple Event Triggers
1 -
Myself Transformation
1 -
Neo
1 -
Neural Networks
1 -
New Event Creation
1 -
New Feature
1 -
Newcomer
1 -
NodeJS
3 -
ODATA
2 -
OData APIs
1 -
odatav2
1 -
ODATAV4
1 -
ODBC
1 -
ODBC Connection
1 -
Onpremise
1 -
open source
2 -
OpenAI API
1 -
Oracle
1 -
Overhead and Operational Maintenance
1 -
PaPM
1 -
PaPM Dynamic Data Copy through Writer function
1 -
PaPM Remote Call
1 -
Partner Built Foundation Model
1 -
PAS-C01
1 -
Pay Component Management
1 -
PGP
1 -
Pickle
1 -
PLANNING ARCHITECTURE
1 -
Plant Maintenance
2 -
Popup in Sap analytical cloud
1 -
PostgrSQL
1 -
POSTMAN
1 -
Practice Systems
1 -
Prettier
1 -
Proactive Maintenance
1 -
Process Automation
2 -
Product Updates
6 -
PSM
1 -
Public Cloud
1 -
Python
5 -
python library - Document information extraction service
1 -
Qlik
1 -
Qualtrics
1 -
RAP
3 -
RAP BO
2 -
React
1 -
Reactive Maintenance
2 -
Record Deletion
1 -
Recovery
1 -
recurring payments
1 -
redeply
1 -
Release
1 -
Remote Consumption Model
1 -
Replication Flows
1 -
Report Malfunction
1 -
report painter
1 -
research
1 -
Resilience
1 -
REST
1 -
REST API
1 -
Retagging Required
1 -
RFID
1 -
Risk
1 -
rolandkramer
2 -
Rolling Kernel Switch
1 -
route
1 -
rules
1 -
S4 HANA
2 -
S4 HANA Cloud
2 -
S4 HANA On-Premise
3 -
S4HANA
6 -
S4HANA Cloud
1 -
S4HANA_OP_2023
2 -
SAC
11 -
SAC PLANNING
10 -
SAP
4 -
SAP ABAP
1 -
SAP Advanced Event Mesh
2 -
SAP AI Core
10 -
SAP AI Launchpad
9 -
SAP Analytic Cloud
1 -
SAP Analytic Cloud Compass
1 -
Sap Analytical Cloud
1 -
SAP Analytics Cloud
5 -
SAP Analytics Cloud for Consolidation
3 -
SAP Analytics cloud planning
1 -
SAP Analytics Cloud Story
1 -
SAP analytics clouds
1 -
SAP API Management
1 -
SAP Application Logging Service
1 -
SAP BAS
1 -
SAP Basis
6 -
SAP BO FC migration
1 -
SAP BODS
1 -
SAP BODS certification.
1 -
SAP BODS migration
1 -
SAP BPC migration
1 -
SAP BTP
25 -
SAP BTP Build Work Zone
2 -
SAP BTP Cloud Foundry
8 -
SAP BTP Costing
1 -
SAP BTP CTMS
1 -
SAP BTP Generative AI
1 -
SAP BTP Innovation
1 -
SAP BTP Migration Tool
1 -
SAP BTP SDK IOS
1 -
SAP BTPEA
1 -
SAP Build
12 -
SAP Build App
1 -
SAP Build apps
1 -
SAP Build CodeJam
1 -
SAP Build Process Automation
3 -
SAP Build work zone
11 -
SAP Business Objects Platform
1 -
SAP Business Technology
2 -
SAP Business Technology Platform (XP)
1 -
sap bw
1 -
SAP CAP
2 -
SAP CDC
1 -
SAP CDP
1 -
SAP CDS VIEW
1 -
SAP Certification
1 -
SAP Cloud ALM
4 -
SAP Cloud Application Programming Model
1 -
SAP Cloud Integration
1 -
SAP Cloud Integration for Data Services
1 -
SAP cloud platform
9 -
SAP Companion
1 -
SAP CPI
3 -
SAP CPI (Cloud Platform Integration)
2 -
SAP CPI Discover tab
1 -
sap credential store
1 -
SAP Customer Data Cloud
1 -
SAP Customer Data Platform
1 -
SAP Data Intelligence
1 -
SAP Data Migration in Retail Industry
1 -
SAP Data Services
1 -
SAP DATABASE
1 -
SAP Dataspher to Non SAP BI tools
1 -
SAP Datasphere
9 -
SAP DRC
1 -
SAP EWM
1 -
SAP Fiori
3 -
SAP Fiori App Embedding
1 -
Sap Fiori Extension Project Using BAS
1 -
SAP GRC
1 -
SAP HANA
1 -
SAP HANA PAL
1 -
SAP HANA Vector
1 -
SAP HCM (Human Capital Management)
1 -
SAP HR Solutions
1 -
SAP IDM
1 -
SAP Integration Suite
10 -
SAP Integrations
4 -
SAP iRPA
2 -
SAP LAGGING AND SLOW
1 -
SAP Learning Class
2 -
SAP Learning Hub
1 -
SAP Master Data
1 -
SAP Odata
3 -
SAP on Azure
2 -
SAP PAL
1 -
SAP PartnerEdge
1 -
sap partners
1 -
SAP Password Reset
1 -
SAP PO Migration
1 -
SAP Prepackaged Content
1 -
sap print
1 -
SAP Process Automation
2 -
SAP Process Integration
2 -
SAP Process Orchestration
1 -
SAP Router
1 -
SAP S4HANA
2 -
SAP S4HANA Cloud
3 -
SAP S4HANA Cloud for Finance
1 -
SAP S4HANA Cloud private edition
1 -
SAP Sandbox
1 -
SAP STMS
1 -
SAP successfactors
3 -
SAP SuccessFactors HXM Core
1 -
SAP Time
1 -
SAP TM
2 -
SAP Trading Partner Management
1 -
SAP UI5
1 -
SAP Upgrade
1 -
SAP Utilities
1 -
SAP-GUI
9 -
SAP_COM_0276
1 -
SAPBTP
1 -
SAPCPI
1 -
SAPEWM
1 -
sapfirstguidance
3 -
SAPHANAService
1 -
SAPIQ
2 -
sapmentors
1 -
saponaws
2 -
saprouter
1 -
SAPRouter installation
1 -
SAPS4HANA
1 -
SAPUI5
5 -
schedule
1 -
Script Operator
1 -
Secure Login Client Setup
9 -
security
10 -
Selenium Testing
1 -
Self Transformation
1 -
Self-Transformation
1 -
SEN
1 -
SEN Manager
1 -
Sender
1 -
service
2 -
SET_CELL_TYPE
1 -
SET_CELL_TYPE_COLUMN
1 -
SFTP scenario
2 -
Simplex
1 -
Single Sign On
9 -
Singlesource
1 -
SKLearn
1 -
Slow loading
1 -
SOAP
2 -
Software Development
1 -
SOLMAN
1 -
solman 7.2
2 -
Solution Manager
3 -
sp_dumpdb
1 -
sp_dumptrans
1 -
SQL
1 -
sql script
1 -
SSL
9 -
SSO
9 -
Story2
1 -
Substring function
1 -
SuccessFactors
1 -
SuccessFactors Platform
1 -
SuccessFactors Time Tracking
1 -
Sybase
1 -
Synthetic User Monitoring
1 -
system copy method
1 -
System owner
1 -
Table splitting
1 -
Tax Integration
1 -
Technical article
1 -
Technical articles
1 -
Technology Updates
15 -
Technology Updates
1 -
Technology_Updates
1 -
terraform
1 -
Testing
1 -
Threats
2 -
Time Collectors
1 -
Time Off
2 -
Time Sheet
1 -
Time Sheet SAP SuccessFactors Time Tracking
1 -
Tips and tricks
2 -
toggle button
1 -
Tools
1 -
Trainings & Certifications
1 -
Transformation Flow
1 -
Transport in SAP BODS
1 -
Transport Management
1 -
TypeScript
3 -
ui designer
1 -
unbind
1 -
Unified Customer Profile
1 -
UPB
1 -
Use of Parameters for Data Copy in PaPM
1 -
User Unlock
1 -
VA02
1 -
Validations
1 -
Vector Database
2 -
Vector Engine
1 -
Vectorization
1 -
Visual Studio Code
1 -
VSCode
2 -
VSCode extenions
1 -
Vulnerabilities
1 -
Web SDK
1 -
Webhook
1 -
work zone
1 -
workload
1 -
xsa
1 -
XSA Refresh
1
- « Previous
- Next »
Related Content
- Handling profile parameter values in SAP NetWeaver and SAP HANA in Technology Blogs by Members
- SAP Datasphere catalog - Harvesting from SAP Datasphere, SAP BW bridge in Technology Blogs by SAP
- Embedding Business Context with the SAP HANA Cloud, Vector Engine in Technology Blogs by SAP
- How to create LLM based Chatbot for SAP HANA Cloud using RAG Application in Technology Blogs by SAP
- Neural Network: Predict "MNIST" data records by a PAL Multilayer Perceptron in Technology Blogs by Members
Top kudoed authors
| User | Count |
|---|---|
| 50 | |
| 5 | |
| 5 | |
| 4 | |
| 4 | |
| 4 | |
| 3 | |
| 3 | |
| 3 | |
| 2 |